Какой 1 признак равенства треугольников. Первый признак равенства треугольников

Конспект урока

«Первый признак равенства треугольников»

(урок №1, 7 класс, по учебнику Атанасяна Л.С.)

Цели урока:

Обучающая:

Ввести понятие теоремы и доказательства теоремы;

Доказать первый признак равенства треугольников;

Научить решать задачи на применение первого признака равенства треугольников.

Развивающая:

Выработать умения сопоставлять, обобщать полученные выводы, оценивать влияние условий на результат;

Развивать логическое мышление учащихся.

Воспитательная:

Выработать умение анализировать данные, выводить логические следствия из данных предпосылок, умение делать выводы;

Выработать умение концентрировать внимание, сосредотачиваться.

Методическая цель: опробовать новый подход к формулировке теоремы, выяснить уловят ли учащиеся момент, когда условия становятся достаточными.

Тип урока: комбинированный.

Оборудование: компьютор, экран, проектор, презентация, линейка, треугольник,

цветные мелки.

Ход урока

Организационный момент : (2 мин)

На предыдущем уроке мы приступили к изучению главы «Треугольники». Выяснили, какие две фигуры, в частности два треугольника называются равными. Сегодня мы выясним, можно ли установить равенство двух фигур не проводя фактического наложения одной на другую, а сравнивая только некоторые элементы этих фигур, в частности как сравнить треугольники.

Повторение пройденного материала: (6 мин)

Повторим материал прошлого урока.

Теоретический опрос по вопросам:

объясните, какая фигура называется треугольником;

начертите треугольник и покажите его стороны вершины и углы;

что такое периметр треугольника?

какие треугольники называются равными?

Каждому учащемуся выдается конвертик, в котором находится 6-7 бумажных треугольников; учащимся предлагается найти среди них равные.

Когда поиск закончен, спросить одного из учеников, как он нашел эту пару. Ученик расскажет, как он накладывал один треугольник на другой.

Выполнение практического задания с последующей устной проверкой:

№1: На доске(или слайде) начерчены ∆DEK, ∆MNP.

Рисунок 1

Назовите углы:

а) ∆DEK, прилежащие к стороне ЕК;

б) ∆MNP, прилежащие к стороне MN.

Назовите угол:

а) ∆DEK, заключенный между сторонами DE и DК;

б) ∆MNP, заключенный между сторонами NP и РМ.

Между какими сторонами:

а) ∆DEK заключен угол К;

б) ∆MNP заключен угол N?

Рисунок 2

Вызываю ученика к доске, он сопровождает свой ответ демонстрацией на чертежах и записью на доске.

3. Изучение нового материала: (16 мин)

Чтобы установить равенство двух треугольников, надо их совмещать или проверить равенство соответствующих сторон и соответствующих углов. Шесть равенств! Но иногда ни совместить, ни проверить все шесть равенств нет возможности. Да это и не нужно, оказывается достаточно установить лишь часть из них. Наша цель - определить, какие из шести этих равенств действительно необходимы.

Итак, перед нами проблема.

Ее решением и займемся.

Рисунок 3

Оказывается справедливо утверждение « Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны». Это утверждение называется «Первый признак равенства треугольников».

А в математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой , а сами рассуждения называются доказательством теоремы.

Какие теоремы нам уже известны?

Свойство смежных углов и свойство вертикальных углов.

Почему же теорема о равенстве треугольников называется признаком?

Признак (по В.Далю) - это знак, отличие, все, почему узнают что-либо. Увидев морозный узор на окне, можно, не выходя из дома, сказать, что на улице холодно. Чтобы узнать, делится ли число 7859467 на 9, не обязательно выполнять деление: можно воспользоваться признаком делимости.

Признак дает возможность устанавливать равенство двух треугольников, не проводя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольников.

Любая теорема состоит из условия и заключения. Как вы понимаете, что может означать словосочетание «условие теоремы», а что - «заключение теоремы»?

Условие - это уже известные факты, о которых говориться в теореме, а заключение - это то, что нужно доказать.

Выделите условие теоремы «Первого признака равенства треугольников».

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.

Выделите заключение теоремы.

То такие треугольники равны.

Итак, докажем первый признак равенства треугольников:

А теперь рассмотрим еще один вопрос. Но сначала послушайте внимательно формулировку: Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны. Как вы думаете, верно ли это утверждение?

Рассмотрим ∆ АВС и ∆АDС.

Рисунок 4

Сторона АВ треугольника АВС равна стороне АD треугольника АDС, сторона АС - общая, и С - общий. Но треугольники не равны. Итак, условие утверждения выполнено, а заключение - нет. Значит утверждение не верно. Обратите особое внимание, на то, что условие «между ними» необходимо!

4. Закрепление нового материала : (10 мин)

Рассмотрим, как же можно применить теорему для решения задач.

Устное решение задач по готовым чертежам, заранее заготовленным на обратной стороне доски или на слайде.

№2:

Для решения каждой задачи вызываю ученика к доске, где он комментирует решение, показывая упомянутые элементы на чертеже. Остальные учащиеся слушают, поправляют, дополняют ответ, если в этом есть необходимость.

Акцентирую внимание учащихся на обязательности содержательной ссылки «треугольники равны по двум сторонам и углу между ними», а не формальной «треугольники равны по первому признаку», выясняю всем ли был понятен ход решения, если возникли вопросы, сама отвечаю на них.

Если в задаче понадобится доказать, что два треугольника равны, чем следует воспользоваться: определением или теоремой?

Конечно, теоремой. Согласно определению нужно треугольники совмещать, а согласно теореме - проверить три равенства.

На рис. АВ = АС, 1 = 2.

а) Докажите, что треугольники АВD и АСD равны;

б) найдите ВD и АВ, если АС=15 см, DC=5 см.

Дано: АВ = АС, 1 = 2,

АС=15 см, DC=5 см.

Доказать:

∆АВD = ∆АСD.

Найти: ВD, АВ.

Доказательство: Прежде чем оформить решение на доске, предлагаю ученикам устно решить задачу. Один ученик комментирует доказательство. Другой - нахождение длин отрезков. А затем записываем решение задачи: я на доске, ученики в тетради.

Возможная запись решения:

Доказательство:

Рассмотрим ∆АВD и ∆АСD.

АВ = АС (по усл.)

АD - общая сторона ∆АВD = ∆АСD (по двум

1 = 2 (по усл.) сторонам и углу между ними)

Словестный комментарий: треугольники АВD и АСD равны по двум сторонам и углу между ними, первый признак равенства треугольников, в котором говориться: «Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.»

ВD =DC =5 см, АВ = АС = 15 см.(как соответственные элементы равных треугольников).

Ответ: ВD =5 см, АВ = 15см.

Выясняю, не возникли ли вопросы по ходу решения.

5. Итог урока: (4 мин)

Итак, давайте повторим:

Какие треугольники называются равными?

Что называется теоремой?

Что называется доказательством теоремы?

Какую теорему мы сегодня доказали? Сформулируйте ее.

Почему теорема называется признаком?

Ученики отвечают на вопросы.

Выставляю оценки за работу на уроке с комментарием.

6. Домашнее задание: (2 мин)

П 15. Вопросы 3 -4 стр. 49-50. №93, 95.

№93. Отрезки АЕ и DC пересекаются в точке В, являющейся серединой каждого из них. А) Докажите, что треугольники АВС и ЕВD равны; б) найдите углы А и С треугольника АВС, если в треугольнике ВDЕ D=470, Е= 420.

№95. На рис. ВС=АD, 1 = 2, а) Докажите, что треугольники АВС и СDА равны; б)Найдите АВ и ВС, если АD =17см, DС=14см.

Список литературы:

Атанасян Л.С., Бутузов В.Ф., и др. Геометрия 7-9 кл. Учебник для 7-9 классов средней школы. - М.: Просвещение, 2006.

Атанасян Л.С., Бутузов В.Ф. и др. Изучение геометрии в 7-9 классах. Методические рекомендации к учебнику. - М.: Просвещение, 2000.

Ковалева Г.И., Мазурова Н.И. Тесты для текущего и обобщающего контроля. Издательство «Учитель» 2008. .

Амелькин В.В., Рабцевич Т.И. Школьная геометрия в чертежах и формулах. 2008.

В этой статье мы расскажем, как можно сформулировать и доказать первый признак равенства треугольников , который проходят в 7 классе.

Формулировка первого признака равенства треугольников

«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»

Сокращенно его называют равенство «по двум сторонам и углу между ними».

Прежде чем перейти к необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.

Что такое треугольник и когда они считаются равными?

Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами ).

На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.

Рисунок 1

Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными ). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.

Доказательство первого признака равенства треугольников

Дано:

Два треугольника: ABC и DEF (рисунок 2).

Рисунок 2

По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).

Доказать , что треугольник ABC равен треугольнику DEF.

Доказательство:

1. Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
2. При этом отрезки СА и СВ наложатся на отрезки FE и FD.
3. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
4. Это в свою очередь даст совмещение вершин А и D, В и Е.
5. Следовательно, треугольники полностью совместятся, а значит, они равны.

Теорема доказана.

Теорема 3.1 (признак равенства треугольников по двум сторонам и углу между ними).Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство. Пусть у треугольников ABC и A 1 B 1 C 1 А= А 1 , AB = A 1 B 1 , АС = А 1 С 1 (рис. 44). Докажем, чтотреугольники равны.

Пусть А 1 В 2 С 2 —треугольник, равный треугольнику ABC, с вершиной В 2 на луче A 1 B 1 и вершиной С 2 в той же полуплоскости относительно прямой A 1 B 1 , где лежит вершина C 1 (рис. 45, а).

Так как A 1 B 1 =A 1 B 2 , то вершина B 2 совпадает с вершиной В 1 , (рис. 45,6). Так как B 1 A 1 C 1 =B 2 A 1 C 2 , то луч А 1 С 2 совпадает с лучом A 1 C 1 (рис. 45, в). Так как A 1 C 1 =A 1 C 2 , то вершина С 2 совпадает с вершиной C 1 (рис. 45, г).

Итак, треугольник A 1 B 1 C 1 совпадает с треугольником А 1 В 2 С 2 , значит, равен треугольнику ABC. Теорема доказана.

Задача (1). Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС = 10 м?

Решение . Треугольники АОС и BOD равны по первому признаку равенства треугольников (рис. 46).

У них углы АОС и BOD равны как вертикальные, а OA=ОВ и OC=OD потому, что точка О является серединой отрезков АВ и CD. Из равенства треугольников АОС и BOD следует равенство их сторон АС и BD. А так как по условию задачи АС = 10 м, то и BD=10 м.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

1) по двум сторонам и углу между ними

Доказательство:

Пусть у треугольников АВС и А 1 В 1 С 1 угол A равен углу А 1 , АВ равно А 1 В 1, АС равно А 1 С 1 . Докажем, что треугольники равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A 1 B 1 C 1 так, чтобы угол A совместился с углом A 1 . Так как АВ=А 1 В 1 , а АС=А 1 С 1 , то B совпадёт с В 1 , а C совпадёт с С 1. Значит, треугольник А 1 В 1 С 1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

2) по стороне и прилежащим к ней углам

Доказательство:

ПустьАВС и А 1 В 1 С 1 - два треугольника, у которых АВ равно А 1 В 1, угол А равен углу А 1 , и угол В равен углу В 1 . Докажем, что они равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A 1 B 1 C 1 так, чтобы AB совпало с A 1 B 1. Так как ∠ВАС =∠В 1 А 1 С 1 и ∠АВС=∠А 1 В 1 С 1 , то луч АС совпадёт с А 1 С 1 , а ВС совпадёт с В 1 С 1 . Отсюда следует, что вершина C совпадёт с С 1. Значит, треугольник А 1 В 1 С 1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

3) по трём сторонам

Доказательство :

Рассмотрим треугольники ABC и A l B l C 1, у которых АВ=А 1 В 1 , BC = B l C 1 СА=С 1 А 1. Докажем, что ΔАВС =ΔA 1 B 1 C 1 .

Приложим треугольник ABC (либо симметричный ему) к треугольнику A 1 B 1 C 1 так, чтобы вершина А совместилась с вершиной A 1 , вершина В — с вершиной В 1 , а вершины С и С 1 , оказались по разные стороны от прямой А 1 В 1 . Рассмотрим 3 случая:

1) Луч С 1 С про-ходит внутри угла А 1 С 1 В 1 . Так как по условию теоремы стороны АС и A 1 C 1 , ВС и В 1 С 1 равны, то треугольники A 1 C 1 C и В 1 С 1 С — равнобедренные . По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠ACB=∠A 1 C 1 B 1 .

2) Луч С 1 С совпадает с одной из сторон этого угла. A лежит на CC 1 . AC=A 1 C 1 , BC=B 1 C 1 , C 1 BC - равнобедренный , ∠ACB=∠A 1 C 1 B 1 .

3) Луч C 1 C проходит вне угла А 1 С 1 В 1 . AC=A 1 C 1 , BC=B 1 C 1 , значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1 .

Итак, AC=A 1 C 1 , BC=B 1 C 1 , ∠C=∠C 1 . Следовательно, треугольники ABC и A 1 B 1 C 1 равны по
первому признаку равенства треугольников.

Теорема доказана.

2. Деление отрезка на n равных частей.

Провести луч через A, отложить на нём n равных отрезков. Через B и A n провести прямую и к ней параллельные через точки A 1 - A n -1. Отметим их точки пересечения с AB. Получим n отрезков, которые равны по теореме Фалеса.

Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Доказательство. AB=CD

1. Проведём через точки A и C прямые, параллельные другой стороне угла. Получим два параллелограмма AB 2 B 1 A 1 и CD 2 D 1 C 1 . Согласно свойству параллелограмма : AB 2 = A 1 B 1 и CD 2 = C 1 D 1 .

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 и равны на основании второго признака равенства треугольников:
AB = CD согласно условию теоремы,
как соответственные, образовавшиеся при пересечении параллельных BB 1 и DD 1 прямой BD.

3. Аналогично каждый из углов и оказывается равным углу с вершиной в точке пересечения секущих. AB 2 = CD 2 как соответственные элементы в равных треугольниках.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы,срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольномтреугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые (рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21), то это прямоугольный треугольник ; стороны a , b , образующие прямой угол, называются катетами ; сторона c , противоположная прямому углу, называется гипотенузой . Если один из углов тупой ( B, рис.22), то это тупоугольный треугольник.


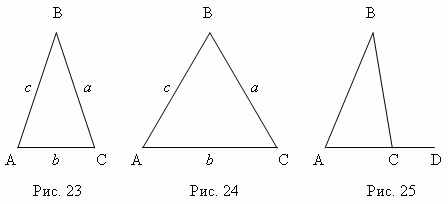
Треугольник ABC (рис.23) - равнобедренный , если две его стороны равны (a = c ); эти равные стороны называются боковыми , третья сторона называется основанием треугольника. Треугольник ABC (рис.24) – равносторонний , если все его стороны равны (a = b = c ). В общем случае (a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний

угол BCD. Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B.

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности (a < b + c , a > b – c ;b < a + c , b > a – c ;c < a + b ,c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O , рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O , рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника (AD , BE , CF , рис.28) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника (AD , BE , CF , рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

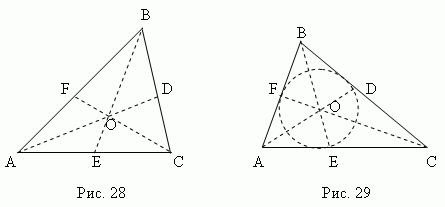
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС (KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга (точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна (a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

c 2 + 4 (ab / 2) = c 2 + 2 ab ,

отсюда ,

c 2 + 2 ab = (a + b ) 2 ,

и окончательно имеем:

c 2 = a 2 + b 2 .

Соотношение сторон в произвольном треугольнике.

В общем случае (для произвольного треугольника) имеем:

c 2 = a 2 + b 2 – 2ab · cos C,

где C – угол между сторонами a и b .